진짜 생전 처음들어봄 !
몬테카를로 알고리즘이랑 부트스트랩이 뭔지 그래도 알고 있어야 할 것 같아서 진짜 간단히 간단히 알아보려고 유투브보고 정리한 내용.
몬테카를로 시뮬레이션
몬테카를로 이름이 되게 생소한데, 모나코의 유명한 도박 도시 "몬테카를로"를 본따서 스타니스와프 울람(수소 폭탄 개발자)이 이름을 지었다고 한다. 알파고 관련 기사를 보여줬는데, 바둑은 경우의 수가 10의 170승올 막대해 컴퓨터가 모두 계산하는게 불가능하다. 그래서 난수를 발생시켜 그 샘플을 얻어서 답을 구하는 방식인 몬테카를로 방법을 사용했다는 기사였다. 즉, 몬테카를로 방법(Monte-Carlo Algorithm)은 수식만으로 계산하기 어려운 문제가 있을 때, 무작위 샘플을 얻은 뒤 그 샘플을 이용해서 답을 구하는 방법이다.
https://www.getnews.co.kr/news/articleView.html?idxno=4256
[알파고 작동원리 분석]① 경우의 수 줄이기 (Search Space) - 글로벌경제신문
[알파고 원리 파헤치기]① 경우의 수(Search Space) 줄이기바둑은 고전 게임 중 탐색 범위가 가장 넓고 보드의 상황을 평가하는 것이 어려워서 인공지능의 가장 큰 숙제 중 하나였다. 체스와 퀴즈게
www.getnews.co.kr
몬테카를로 시뮬레이션 예시
원의 넓이를 구하는 경우에 원 안에 점을 찍어서 원의 내부에 찍힌 확률을 계산하면 원의 넓이를 근사적으로 구할 수 있다.
예를 들어, 반지름이 1인 원을 그리고 인접하는 사각형을 그린다. 사각형에 임의의 점을 찍으면 대략 0.8의 확률로 원안에 점이 찍힌다. 그러면 사각형의 넓이가 4이니까 0.8 X 4 = 3.2가 된다. 반지름이 1인 원의 면적은 3.14 이니까 근사치로 구할 수 있다.
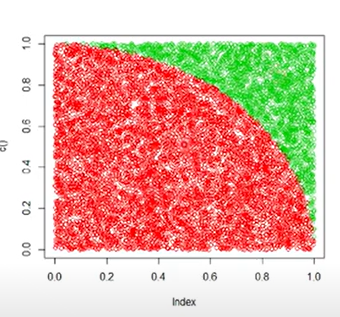
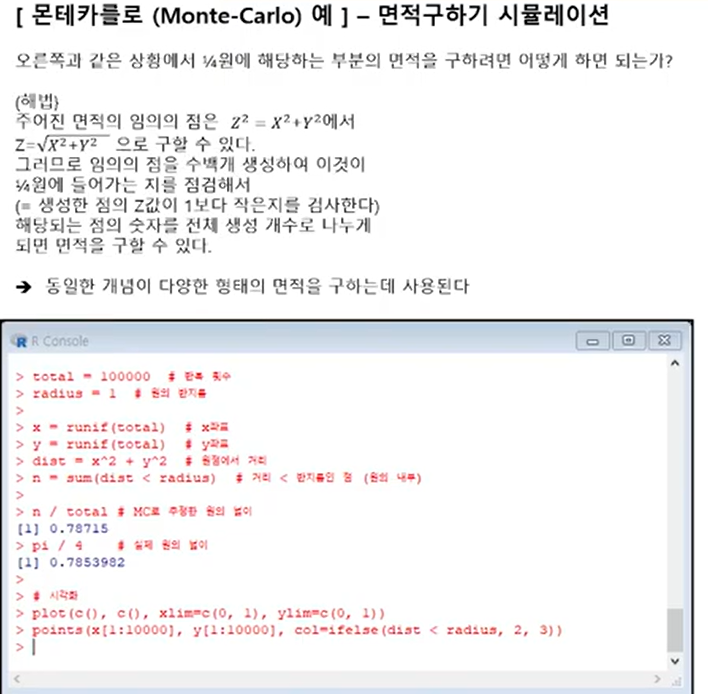
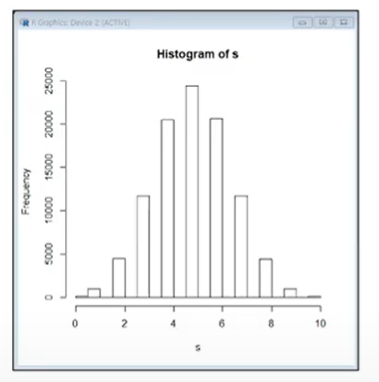
또 다른 예로는 이항분포에서 누적 확률 분포를 구할 때, 이항 분포는 연속된 n번의 독립시행에서 각 시행이 확률 p를 가질때의 이산확률분포이다. 예를 들어 앞면이 나올 확률이 60%인 동전을 100번 던졌을때 그 중에서 앞면이 x번 나올 확률같은 것이 이항분포이다.
이항분포의 누적확률분포를 0에서 X까지의 확률을 모두 더한 것을 말한다. 즉, X=2의 누적확률은 p(x=0) + p(x=1) + p(x=2)가 된다.
이항분포의 계산방법은 알려져있지만, 실제 계산을 번거로워 몬테카를로 방법을 이용해서 간단히 풀 수 있다.

마르코브체인 몬테카를로 알고리즘(Markov Chain Monte Carlo method : MCMC)
마르코브체인(Markov Chain)은 어떤 상태에서 다른 상태로 넘어갈 때, 바로 전 단계의 상태에서만 영향을 받은 확률 과정을 말한다. MCMC에서는 가장 마지막에 뽑힌 샘플이 다음 번 샘플을 추천 해준다는 의미에서 단어가 들어갔다고 보면 좋을 것 같다.
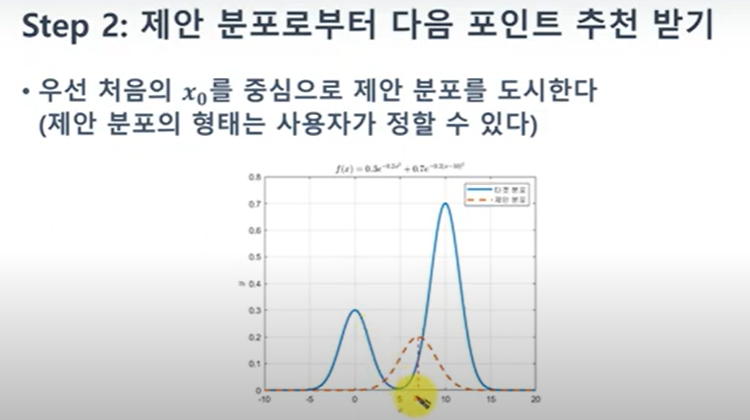
MCMC를 이용한 샘플링 과정
1. 첫 샘플을 랜덤하게 선정
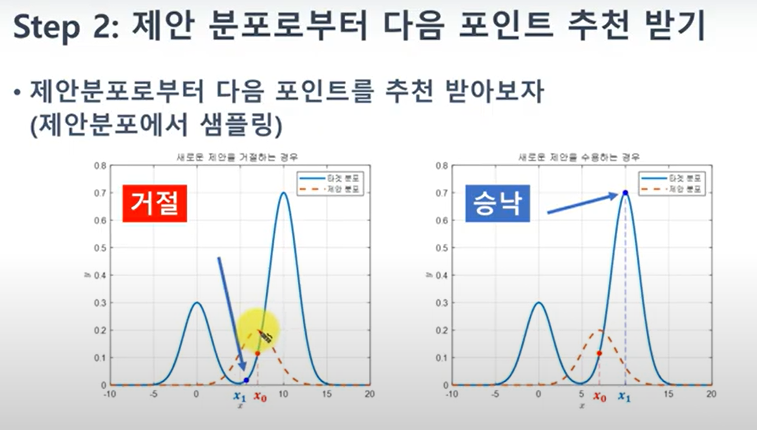
2. 선정된 샘플에 의해 그 다음 번 샘픙을 추천(제안분포 잉ㅇ)
3. 특정 기준에 따라 추천된 샘플을 ACCEPT or REJECT
4. 2~3을 무수히 많이 시도
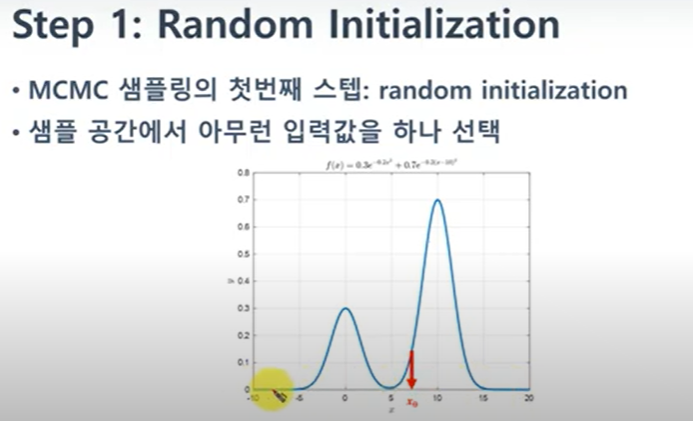


간단한데 또 생각해보면 넘 어렵...
출처 맨 아래에 있는 깃허브 시간나면 보기 !!
출처 :
https://youtu.be/-M4cBYQpjtk
https://youtu.be/drZt9XLjIRw
https://youtu.be/5QAfQZjCrRM
https://angeloyeo.github.io/2020/09/17/MCMC.html
'나는야 데이터사이언티스트 > 통계' 카테고리의 다른 글
| 베이지안(Bayesian Inference) 쉽게 이해하기 (1) | 2021.03.04 |
|---|---|
| 상관분석(Correlation Analysis) 쉽게 이해하기 (2) | 2021.01.19 |
| [통계]표본 크기 계산 방법 (0) | 2020.11.17 |
| 데이터 전처리 필요성 및 방법(Feature Engineering, EDA) (0) | 2020.11.10 |
| 모델 성능 평가 지표 (회귀 모델, 분류 모델) (0) | 2020.06.24 |