모델 성능 평가
모델을 만드는 이유는 일반화를 통해 미래(미실현) 예측을 추정하고자 하는 것이다. 그래서 우리는 train data로 학습시키고, 알고리즘을 계속해서 수정하고, 주어진 가설 공간에서 최고의 성능을 발휘하는 모델을 선택함으로써 예측 성능을 높힌다.
그렇게 여러가지로 만든 모델을 서로 비교해서 좋은 모델을 선택해야하는데 이때 모델 평가 지표를 사용해서 성능을 평가한다. 연속된 값에 대한 평가 지표(회귀 모델)와 분류에 대한 평가 지표를 다르게 사용한다.

회귀 모델
● MAE(Mean Absolute Error)
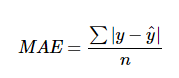
모델의 예측값과 실제값의 차이를 모두 더한다는 개념
- 절대값을 취하기 때문에 가장 직관적으로 알 수 있는 지표이다.
- MSE 보다 특이치에 robust한다. (robust란 ? 이상치에 대한 저항도 가지고 있고, 데이터 특성을 잘 나타냄)
- 절대값을 취하기 때문에 모델이 underperformance 인지 overperformance 인지 알 수 없다.
- underperformance: 모델이 실제보다 낮은 값으로 예측
- overperformance: 모델이 실제보다 높은 값으로 예측

● MSE(Mean Squared Error)

제곱을 하기 때문에 MAE와는 다르게 모델의 예측값과 실제값 차이의 면적의 합이다. 이런 차이로 특이값이 존재하면 수치가 많이 늘어난다.
- 특이치에 민감하다

● RMSE(Root Mean Squared Error)

MSE에 Root 씌운 것.
- RMSE를 사용하면 오류 지표를 실제 값과 유사한 단위로 다시 변환하여 해석을 쉽게 한다.
● MAPE(Mean Absolute Percentage Error)
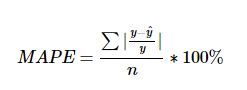
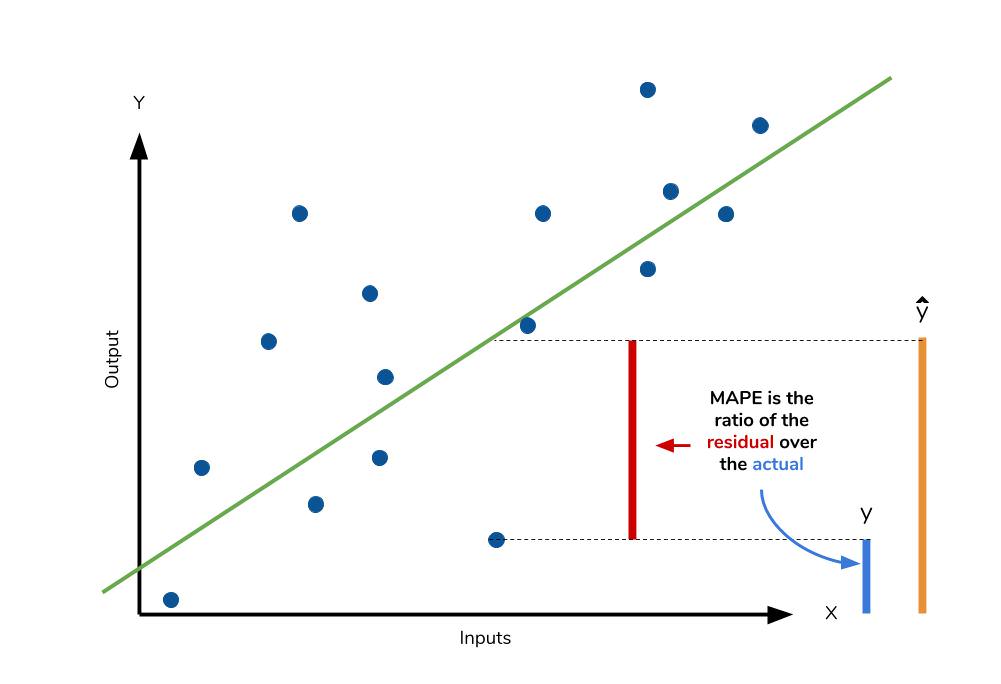
MAPE는 MAE를 퍼센트로 변환한 것
- MAE와 마찬가지로 MSE보다 특이치에 robust 한다.
- MAE와 같은 단점을 가진다.
- 추가적으로 모델에 대한 편향이 존재한다.
- 이 단점에 대응하기 위해 MPE도 추가로 확인하는게 좋다.
- 0 근처의 값에서는 사용하기 어렵다.
● RMSLE(Root Mean Square Logarithmic Error)

RMSE에 로그를 취해 준 것
- 아웃라이어에 robust 하다. RMSLE는 아웃라이어가 있더라도 값의 변동폭이 크지 않다.
- 상대적 Error를 측정해준다. RMSE와 달리 RMSLE는 예측값과 실제값의 상대적 Error를 측정해준다.
- Under Estimation에 큰 패널티를 부여한다. 즉, 예측값이 실제값보다 작을 때 패널티 부여.
● R2 Score(Coefficient of Determination, 결정계수)

상대적으로 얼마나 성능이 나오는지를 측정한 지표.
- 다른 성능 지표인 RMSE나 MAE는 데이터의 scale에 따라서 값이 천차만별이기 때문에 절대 값만 보고 바로 성능을 판단하기가 어려운데, 결정계수의 경우 상대적인 성능이기 때문에 이를 직관적으로 알 수 있다.
● EVS
EVS를 아시는 분 제발 댓글 달아주세요.
분류 모델
● Accuracy(정확도), Precision(정밀도), Recall(재현율), F1 Score, Fall-out
이것을 이해하는데 있어 먼저 confusion matrix를 봐야한다. confusion matrix는 contingency table 또는 an error matrix라고도 불리는데 주로 알고리즘의 성능을 평가할 때 사용된다.

- True Positive(TP) : 실제 True인 정답을 True라고 예측 (정답)
- False Positive(FP) : 실제 False인 정답을 True라고 예측 (오답)
- False Negative(FN) : 실제 True인 정답을 False라고 예측 (오답)
- True Negative(TN) : 실제 False인 정답을 False라고 예측 (정답)
이 행렬을 토대로 정확도, 정밀도, 재현율을 알아보자.
- Accuracy(정확도)

정확도란 전체 중에서 정답을 맞춘 비율이다. True던지 False던지 상관없이 그냥 정답을 맞춘 비율. 1에 가까울 수록 좋다. 이런 Accuracy(정확도)의 한계점은 무엇일까 ? 예를 들어보자.
100명의 사람이 악성 종양 검사를 받았다고하자. 이떄 진짜 악성 종양을 가지고 있는 사람이 5명이다. Accuracy(정확도)는 전체 개수 중 양성을 양성이라 말하고, 음성을 음성이라고 말한 개수의 비율이다. 우리가 만든 모델에 넣었을 때, 정확도가 90%가 나왔다. 정확도 90%를 살펴보니 악성 종양을 가진 사람은 맞추지 못했고 악성 종양을 가지지 못한 사람을 90%까지 맞췄다. 이것은 좋은 모델이라고 할 수 있는가 ?
Accuracy는 bias에 관해 단점을 가진다. 이런 상황을 정확도 역설(Accuracy Paradox)라고 부른다.
그래서 이렇게 실제 데이터에 Negative 비율이 너무 높아서 희박한 가능성으로 발생할 상황에 대해 제대로 된 분류를 해주는지 평가해줄 지표는 바로 Precision(정밀도)와 Recall(재현율)이다.
- Precision(정밀도)

정밀도란 모델이 True라고 분류한 것 중에서 실제 True인 것의 비율이다. PPV(Positive Predictive Value)라고도 불리고 1에 가까울 수록 좋다. 정밀도의 한계점도 있다. 위의 예를 다시 사용해보자.
정밀도는 양성이라고 판정한 환자 중에서 실제 양성인 수의 비율을 말한다. 환자 100명 중에 확실한 2명만 악성 종양을 가지고 있다고 예측한다면 Precision은 100%가 나오게 된다. 이것 또한 이상적인 모델이 아니다. 양성 환자를 몇 명 놓쳤지만 정밀도는 100% 이기 때문이다.
- Recall(재현율)
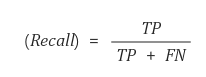
재현율이란 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율이다. sensitivity 또는 hit rate라고도 불리고 1에 가까울 수록 좋다. 재현율은 단점은 정밀도와 비슷하다.
재현율은 전체 양성 수에서 검출된 양성 수의 비율을 뜻한다. 앞에서 사용했던 예제에서는 5명 중에 2명을 양성이라고 검출했으니까 40%의 확률인것이다. 여기서 Precision과 Recall 둘다 높으면 가장 좋은 방법이겠지만 이 둘은 반비례하는 경향이 있다. 이를 보완하기 위해 이 둘의 조화평균을 사용하는 F1 score이 등장했다.
- F1 score

Precision과 Recall의 조화평균이다. 즉, F1 socre가 높아야 성능이 좋다.
흔히 말하는 평균(산술평균)을 쓰지 않고 조화평균을 구하는 이유는 recall, precision 둘 중 하나가 0에 가깝게 낮을 때 지표에 그것이 잘 반영되도록, 다시말해 두 지표를 모두 균형있게 반영하여 모델의 성능이 좋지 않다는 것을 잘 확인하기 위함이다.
예를 들어 recall, precision이 각각 1과 0.01이라는 값을 가지고 있다고 하자. 산술평균을 구하면 (1 + 0.01) / 2 = 0.505, 즉 절반은 맞히는 것처럼 보인다. 그러나 조화평균을 구해보면 2 * (1 * 0.01) / (1 + 0.01) = 0.019가 된다. 낮게 잘 나온다.
- Fall-out

Fall-out은 FPR(False Positive Rate)으로도 불리며 실제 False 중에서 모델이 True라고 예측한 비율이다. 즉, 모델이 실제 false data인데 True라고 잘못 예측(분류)한 것으로 말할 수 있다. 아래는 이제껏 배웠던 5가지 모델 비교 중 4가지를 이해하기 쉽도록 시각화로 표현했다.
▼
▼
▼
▼

● Log Loss
모델이 예측한 확률 값을 직접적으로 반영하여 평가한 것이다. 확률 값을 음의 log 함수에 넣어 변환을 시킨 값으로 평가한다. 값이 적을수록 좋은 값이다.
예측 확률이 100%일때 -log(1.0) = 0이 되고, 80% 확률일 때 -log(0.8) = 0.22314가 된다. 즉, 예측을 못 할수록 값은 더 높아지는 것이다. 아래의 그래프를 보면 확률이 낮아질 수록 Log Loss 값이 기하급수적으로 증가하는 것을 볼 수 있다. 이런식으로 Log Loss는 확률이 낮을 때 패널티를 더 많이 부여하기 위해 음의 로그 함수를 사용한다. Log Loss는 확률 값을 음의 로그를 취해 모두 더하고 1/n해서 평균을 내면된다.

▼
▼
▼
● Cost Matrix Gain
Cost matrix is similar to the confusion matrix except the fact that we are calculating the cost of wrong prediction or right prediction.
Confusion matrix와 비슷한 것 같은데 정확히는 잘 모르겠다.
● Cumulative Lift Chart(누적 향상도)
Gain Chart 라고도 부르며 Lift(향상도)를 이해해야한다. Lift(향상도)는 B를 그냥 구매할 때보다, A를 구매한 사람이 B를 구매할 확률이 얼마나 더 높은가를 생각하면 된다. 더욱 이해하기 쉽게 지지도, 신뢰도, 향상도를 함께 설명해보자.
지지도 : 전체 구매자 중에서 Green 과 Red를 동시에 구매한 사람의 비율은 0.2. 즉 20% 확률이다.
신뢰도 : Green을 구매한 사람들이 Red를 구매한 확률 1.0. 즉 100% 확률이다.
향상도 : Green을 구매한 사람이 Red를 구매하게 될 가능성은 그냥 Red를 구매할 때보다 1.67배나 높아진다.
다시말해 Green을 구매했을 때 Red를 구매할 가능성이 높다는 것은 이 경우에 관해서 더 마케팅에 집중하게 되면 좋을 것이라는 이야기이다. Cumulative chart는 데이터 각각의 Lift(향상도)를 구하고 cumulative를 해주면 된다.

▼
▼
▼
●ROC AUC (Receiver Operating Characteristic Curve & Area Under the Curve)
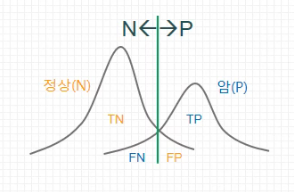
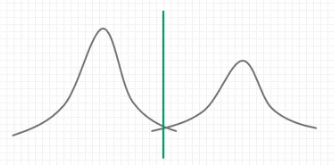
ROC 곡선은 Binary Classifier System(이진 분류 시스템)에 대한 성능 평가 기법이다. 면적(AUC)의 크기로 더 큰 것이 좋다고 할 수 있다. 아래 그림에서는 빨간색이 더 좋은 성능을 가진다고 할 수 있다.

아래의 그림을 볼 때, 왼쪽보다 오른쪽 그림이 더욱 분리하기 쉽다. 이것이 무슨 의미냐면 암환자를 판별할 때, 확실하게 판별하면 좋겠지만 왼쪽 그림의 초록색 선처럼 판단이 불분명한 부분이 있을 수 밖에 없다. 그래서 오른쪽 그림같이 분포가 많이 겹치지 않을 때 판별을 더 잘할 수 있게 하는데 이것이 위에서 말한 빨간색 성능이 더 좋은 그래프인 것이다.
이것은 또 다른 말로 분포가 많이 겹치면 직선에 가까워 진다고 할 수 있다.
위의 ROC 수식은 이렇게 나타낼 수 있는데 정말로 사용하는 게 아니면 한번도 안해볼 것 같다. 요즘은 컴퓨터로 해주니까.... 뭐 어쨋든 하는 방법은 알아놓아야하므로 관련 URL을 남겨놓는다.

ROC (Receiver Operating Characteristic) Curve 완벽 정리!
이전에 스터디 하면서 작성해놓은 발표 자료를 다시 한번 정리해서 블로그에 기록해두고자 한다. 이 개념은...
blog.naver.com
ROC, AUC의 관한 부분은 매번 헷갈리니까
사용할 때마다 유투브를 보자 !
▼
▼
▼
출처 :
https://sumniya.tistory.com/26
http://hleecaster.com/ml-accuracy-recall-precision-f1/
https://partrita.github.io/posts/regression-error
https://newsight.tistory.com/259
'나는야 데이터사이언티스트 > 통계' 카테고리의 다른 글
| [통계]표본 크기 계산 방법 (0) | 2020.11.17 |
|---|---|
| 데이터 전처리 필요성 및 방법(Feature Engineering, EDA) (0) | 2020.11.10 |
| 교차검증(Cross-Validation) 쉽게 이해하기 (0) | 2020.06.04 |
| AIC, BIC, Mallow's Cp 쉽게 이해하기 (0) | 2020.06.01 |
| 최대우도추정법 쉽게 이해하기 (2) | 2020.05.13 |